Week 2: Volume II, Chapter 42 - Curved Space

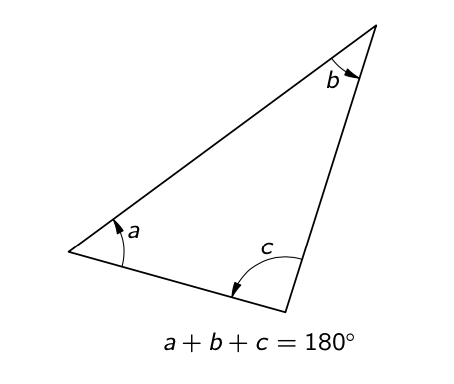
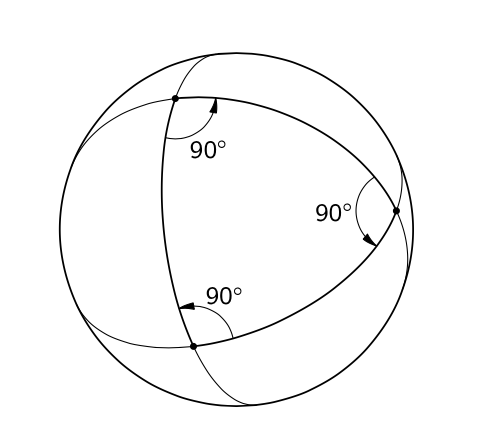
The notion that space is curved is somewhat colloquially thrown around by folks touching on the theories of Einstein, but what does it really mean for space to be curved and how do we know that our space (rather our space-time) is curved? The definition of curved space is actually quite simple; curved space is space that does not obey the laws of geometry set forth by Euclid. For example, Euclid told us that the sum of the interior angles of any triangle must add up to 180 degrees as seen below in Figure 1. However, we can easily see in Figure 2 that by drawing a triangle on the surface of a sphere (a curved space), we obtain a triangle where the interior angles add up to be greater than 180 degrees. Similar thought experiments can be done for just about any shape you can think of.

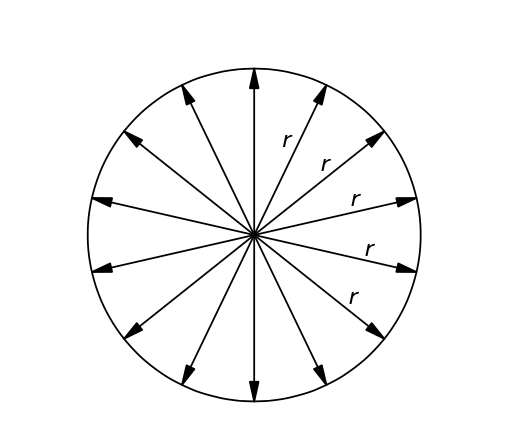
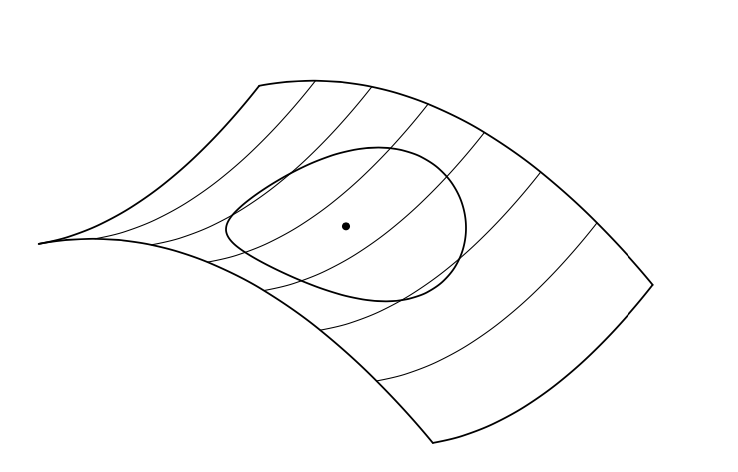
Imagine a bug that lives on a 2 dimensional space and is familiar with Euclidean geometry (the geometry of flat space). The bug knows from Euclid that the circumference of a circle ought to be 2πr. So, in an attempt to find out if his space is curved or not, the bug starts at an arbitrary point in his space and walks some distance r from this point. He then returns to his starting point and repeats the process several times creating a circle from each of the endpoints of his jourrneys as seen in Figure 3. The bug then walks around the circumference of the circle and meticulously measures it's total length. If the circumference of the circle is equal to 2πr then the bug knows that he lives in a flat space. However, if the circumference is any more or any less than 2πr, the bug concludes that his space must be curved. One example of what this may look like is seen in Figure 4. It is clear to us 3 dimensional beings that the bug's 2 dimensional space is curved. The bug however, has no knowledge of what exists outside of his 2 dimensional space. Even so, he was able to discover that his space is curved and exists in a higher dimension. The key takeaway here is that you do not need to exist as a higher dimensional being to infer that your space is curved.

Einstein's astute observation in his General Theory of Relativity was that mass curves our space. In fact, we can perform an analagous experiment to the bug and imagine we start at the center of the earth and travel outwards by a direction r over and over until we form a sphere from all of our end points. Euclid tells us that the surface area of a sphere ought to be 4πr². If we now measure the surface area of this sphere we would find that it corresponds to a sphere with a radius 1.4 millimeters larger than the distance we traveled from the center of the earth. In hindsight, we are quite lucky to exist on a planet that does not have enough mass to significantly curve space-time because this allowed Euclid to set forth his laws of geometry that were based on his observations in a nearly flat space. If we existed near the surface of a black hole, things would have been much more complicated and we may not understand the geometry of flat space that now serves as a reference for us to determine if our space is in fact curved.